ELS NOMBRES AL LLARG DE LA HISTÒRIA

El nombre π a Egipte

 

A Egipte trobem una de les fonts matemàtiques més antigues que fan referència al nombre π. Es tracta del papir de Rhind[1] , que data aproximadament de l’any 1.650 aC. Es tracta d’una còpia realitzada per un escriba anomenat Ahmes[2] a partir d’un document original molt més antic, que un antiquari escocès, anomenat Alexander H. Rhind, va comprar el 1858 a Luxor (Egipte), i d’aquí li ve el nom. El papir fa uns 5 metres de llarg i 33 cm d'ample i està escrit per les dues cares. Consta de 87 problemes escrits en escriptura hieràtica que tracten aspectes matemàtics diversos d’àlgebra, geometria i trigonometria.

 

La referència indirecta al nombre π es pot trobar al problema número 50, que diu: “Un camp circular té un diàmetre de 9 khet[3], quina és la seva àrea?”.

• El mateix papir Rhind proporciona el sistema per a calcular l’àrea a partir de l’expressió: A= , on d és el diàmetre.

• Actualment calcularíem l’àrea del camp circular de la següent manera: A=π· 2, amb d=9.

• Si igualem les dues expressions obtenim un valor aproximat del nombre π igual a: π= 3,160493827

 

 

El nombre π a Grècia

 

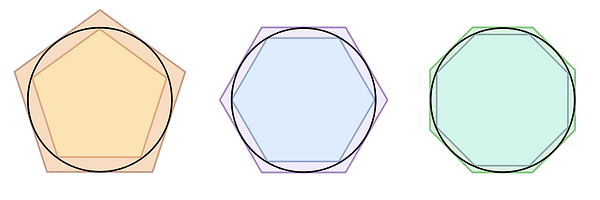
Arquímedes va arribar a una bona aproximació a partir del que ara es coneix com a “mètode clàssic”[4]. Arquímedes pensava que calcular la longitud d’una circumferència a partir del seu diàmetre no era gens fàcil, però si dibuixava un polígon inscrit i un altre circumscrit a la circumferència i calculava els seus perímetres, sabia amb certesa que la longitud de la circumferència es trobava compresa entre els dos perímetres: Pinscrit  ≤ Lcircumferència ≤ Pcircumscrit.

 

A continuació podem veure el mètode emprat per Arquímedes amb polígons de 5, 6 i 8 costats  respectivament[6]:

 

 

 

 

 

 

 

 

 

 

 

 

Fent els números pel polígon de 6 costats o hexàgon s’obté: 3 ≤ π ≤ 3,45. No resulta una aproximació gaire precisa, però si anem ampliant els costats dels polígons inscrit i circumscrit cada vegada serà millor. Arquímedes va arribar a calcular-ho amb un polígon de 96 costats  i va trobar una aproximació de π ≈ 3,14.

 

 

El nombre π a la Bíblia

 

A la Bíblia trobem una de les primeres aproximacions al nombre π. Al primer llibre dels Reis[7] (I Re 7, 23) podem llegir[8]: “Després va fer l’anomenat “Mar de bronze”, un dipòsit rodó de bronze fos. Feia deu colzades de diàmetre, trenta de perímetre i cinc de profunditat.” Si tenim en compte que el perímetre del dipòsit rodó equival al diàmetre multiplicat pel nombre π, amb una simple divisió podem deduir que el valor associat a π és de π= 3 .

 

Pels historiadors[9] del nombre π, aquesta aproximació no té gaire valor, donat que el text bíblic només fa una descripció dels objectes que el rei Salomó va manar construir pel seu Temple, no es tracta en cap cas d’un intent seriós de calcular π. En aquest sentit, les aproximacions que van aconseguir els egipcis, els grecs i els xinesos, entre d’altres, van ser molt més exactes.

 

 

El nombre π a Xina

 

L’atracció pel càlcul del nombre π també va arribar a la Xina on nombrosos matemàtics van fer importants aportacions. Així, Zhang Heng[10] (78-139 d.C.), un destacat astrònom que va inventar un detector de terratrèmols, va treballar amb una esfera inscrita dintre d’un cub i va fer els càlculs matemàtics utilitzant com a aproximació del nombre π: π = 3,1622 ...

 

Un segle després, un altre astrònom xinès, Wang Fang (217-257 d.C.) també es va interessar per les matemàtiques. L’any 250 va escriure la següent aproximació del nombre π:  π =3,1555.

 

Una aportació molt destacada serà la del matemàtic xinès Liu Hui[11] (aprox. 220-280 d.C.). L’any 263 d.C. va editar i va publicar un llibre amb solucions pels problemes matemàtics presentats en el famós llibre conegut com Els Nou Capítols de l'Art Matemàtica i va desenvolupar un mètode d’aproximació a π treballant amb polígons inscrits en un cercle de diàmetre conegut.

 

Inicialment Liu Hui va recomanar l’aproximació π ≈ 3,14, però treballant amb un polígon de 3.072 costats va arribar a una altre aproximació del nombre π més precisa: π ≈ 3,141592104...

 

A finals del segle V, Zu Xongzhi[12] (429-500 dC), astrònom i matemàtic, creador de nous calendaris, va calcular que el valor de π estava entre el que va anomenar “valor per defecte” i “valor per excés”: 3,1415926 < π < 3,1415927. També va donar dues aproximacions racionals: π ≈22/7   i π ≈355/113  .

 

 

Aplicacions i usos de π

 

Actualment, el nombre pi es pot trobar, entre molts altres llocs i situacions a[13]:

• La doble hèlix de l'ADN

• L'arc de Sant Martí, la pupil·la de l'ull, o quan una gota de pluja cau en aigua, π emergeix en els anells estesos.

• La relació entre la longitud real d'un riu i la seva línia recta des de la font de naixement fins a la boca tendeix a acostar-se a π. (Demostrat per Einstein)

• La navegació basada en sistemes de posicionament global (GPS)

• Problemes de geometria: dibuix, física, enginyeries, etc.

• Càlcul de les àrees del casc de les longituds de les aeronaus.

• Senyals: ràdio, televisió, radar, telèfons, etc.

• Navegació: quan els avions volen grans distàncies en realitat estan volant fent un arc al voltant d’un cercle.

 

 

 

 

 

[1] Més informació a: http://ca.wikipedia.org/wiki/Papir_de_Rhind  

 

[2] Ahmes: http://es.wikipedia.org/wiki/Amhes 

 

[3] 1 khet equival aproximadament a 50 m.

 

[4] Aquest mètode va ser ideat per Eudoxo de Cnido i es denomina “mètode d’exhausció”.

 

[5] Més informació a: http://ca.wikipedia.org/wiki/Arqu%C3%ADmedes_de_Siracusa

 

[6] Font de la imatge: http://ca.wikipedia.org/wiki/Fitxer:Archimedes_pi.svg 

 

[7] Aquest llibre va ser escrit aproximadament l’any 900 a.C.

 

[8] “Bíblia catalana traducció interconfessional”, Barcelona 1994, pàgina 452.

 

[9] Navarro, Joaquín, “Los secretos del número π”, Ed. RBA, Barcelona 2010, pàgina 18.

 

[10] Més informació de Zhang Heng a: http://ca.wikipedia.org/wiki/Zhang_Heng

 

[11] Es pot consultar la biografia, l’obra i veure alguns exemples de problemes matemàtics resolts a: http://divulgamat2.ehu.es/divulgamat15/index.php?option=com_content&view=article&id=10423&directory=67

 

[12] Més informació a: http://ca.wikipedia.org/wiki/Zu_Chongzhi

 

[13] Aplicacions de p: http://www.buenastareas.com/ensayos/Aplicaciones-De-Pi/7192500.html